教科書レベルとは
教科書レベル＝最大限レベル
教科書レベルという表現は、標準レベル以下の言い換えのように浸透しています。
しかし例えば生徒の「覚えられない！」という嘆きには、（教科書の内容を）覚えられない！という重要な目的語が抜けています。
教科書は指導要領に沿って記述しています。学習内容の最大限まで載せてあるということは、教科書レベル＝最上級レベルを意味します。このレベルへの到達は、入試問題が「すべて」解けるための必要条件です。
このことから教科書の内容を理解し記憶することは入試対策の90%を占めるといえます。言い換えれば、９割は教科書の理解があれば正解を得るということです。500点満点であれば450点が取れます。残りの10％を解かなければならない人はほんの一握り。それよりも７割でＯＫのところを８割、５割でＯＫのところを６割正解できるように私たちは指導しています。
教科書の記述は非常によく考えられています。読み込めば読み込むほど、配置順まで工夫されていることが分かります。これはやはり、日本の教育＝長い年月にわたる英知の結集といえるでしょう。
学校の授業で教科書の順番を無視し、入れ替えることがあります。しかし、困る場面に必ず遭遇するため、順序変更がうまく機能していると思ったことは一度もありません。
応用問題も解ける［高校入試編］
正解率の低い「応用問題」は教科書に存在するのか、一例を挙げご説明いたします。ご一緒にお考えください。
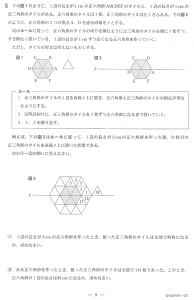
2017年千葉県公立高校数学前期大問５（最終問題）（7点分）
「三角形をぐるぐると反時計回りに並べて六角形を作ります。全部で何枚並べたでしょうか。ただし枚数は２周目（＝1辺2cm）からカウントします。」と言っています。
では、枚数を書き出します。
- １辺1cmは6枚（これは総数に含まない）
- １辺2cmは1～18番で18枚→（1～3番の）3枚が6辺分 → 18枚
- １辺3cmは（19から24番の）5枚が6辺分 → 30枚+前回18枚→４８枚
- １辺4cmは7枚が6辺分 → 42枚+前回48枚→90枚
- １辺5cmは9枚が6辺分 → 54枚+前回90枚→１４４枚
- １辺6cmは11枚が6辺分 → 66枚+前回144枚→210枚
はい、できました！答えは（１）48（２）5 です。
この背景にあるのは中学１年生の数学の教科書56ページの上部です（船橋市採択の教科書）
法則を探して小学校で学ぶ程度の算式を順番に作らせます、ただそれだけです。教科書にならって表にすると、
| １辺 | 並べた枚数 |
| 1cm | (1)×6 －6 |
| 2cm | (1+3)×6 －6 |
| 3cm | (1+3+5)×6 －6 |
| 4cm | (1+3+5+7)×６－6 |
| 5cm | (1+3+5+7+9)×6 －6 |
| 6cm | (1+3+5+7+9+11)×6 －6 |
このように授業を進めています。
ところで、千葉県は後日正答率を発表します。この問題は、どれ程の正答率だと思われますか。
（１）たったの３８％＝３人に１人＝偏差値５３以上 （２）２６％＝４人に１人＝偏差値５７以上
さらにこの問題は（３）へ２問続きますが、正答率は順番に、８％（＝偏差値６５以上）、４％（＝偏差値６８以上）です。
試験時間も限られますから（１）と（２）が出来れば十分ではないでしょうか。
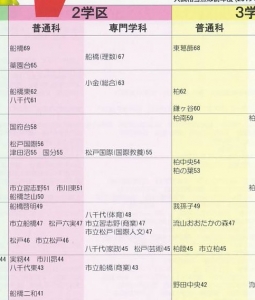
［ご参考］高校ランク（数字は偏差値）
応用問題＝正答率の低い問題＝教科書レベル！
であります。教科書レベルで大丈夫？？？ ご心配なく、大丈夫です。取れる問題で必ず正解し、捨てる問題はバッサリ切る。このテクニックを指導いたします。え？じゃ、教科書丸暗記で大丈夫じゃないの？？？ 残念ながら教科書の太文字を暗記するだけでは得点に繋がりません。上手な暗記のテクニックも指導いたします。
この問題の続きを補足します
1+3+5+7+9+11+・・・１から始まる奇数の足し算は、足した個数の２乗になります。たとえば、
1+3+5+7+9+11＝36＝6×6＝6(個)の２乗
式で書くと、奇数をｎ個足し算したらｎ² です。表を参考にn(cm)の枚数は、
ｎ²×6 －6
たとえ1辺50cmでも50×50×6－6＝14,994枚と簡単に計算ができます。
奇数の足し算はｎ²、偶数の足し算はｎ²＋ｎを知っていればラクですが、知らなくてもOK！明研進学会は「知らなくても問題無し！」とする塾です。そもそもこの問題はこんな知識を要求していません。（念のため生徒に公式は伝えますが、）覚えたい人だけ覚えればいい。
それよりも、知らなくても良いことを塾で知り、それを学校で自慢げに話す生徒になって欲しくありません。覚えた生徒には「そっと使いなさい！」と必ず添えます。偶数の足し算がｎ²＋ｎという知識より、なぜそうなるのか、という過程のほうが数万倍重要です。また心配せずとも、これらの知識は高校で学びます。塾が教える余計な知識は、すべて高校で学ぶものばかりです。高校の先取りに意味があるとは思いません。知識欲を満たすことは大いに結構ですが、上から目線の生徒になって欲しくありません。
応用問題も解ける［大学入試編］
2018年青山学院大（英文科）の問題
What is your image of an ideal city? (Feel free to use your imagination.)
「あなたの理想とする都市のイメージを述べてください。想像でＯＫ」と言っています。
英語表現Ⅱの教科書（船橋啓明ほか採択）Lesson4に、
都会と田舎の特徴を書き出し、それぞれの魅力を語って「対比」の組み立て方を学びます。これを基に、
（１）自然と共生することが理想［起］
（２）だから田舎がよい［承］
（３）しかし都会は失いたくない［転］
（４）現住する船橋は田舎も都会もあり理想だったと気付く［結］
こう組み立て直せば、教科書の文章をタップリ使え、物語性とオチも完璧！
（１）本文の６番を拝借します Rural areas have fresh air and water, and people are surrounded by the beauty of nature.
（２）教科書の提案通り、つなぎの文を加えます So I guess an ideal city is in the country side.
（３）本文の３番５番６番を合体します On the other hand, cities have cultural facilities such as museums, galleries, theaters, concert halls, and usually have a good transportation system. I need all of them.
（４）教科書 Lesson6（文章の結び方） にある熟語を２つ使って結論を作ります To my surprise, Funabashi, which I live in now, has an urban area and a rural area. This means my town is already an ideal city. In short, my image of an ideal city is Funabashi.
数えると50語を大きく超えているので短縮し、叙述的にするために、２回書いた「船橋」の１回目を「わがまち」と濁します。
Rural areas have fresh air and water, and people are surrounded by the beauty of nature. So I guess an ideal city is in the country side. On the other hand, I need cultural facilities and a good transportation system. To my surprise, my town has all of them and is in a rural area. In short, my ideal city is Funabashi. (58語)
田舎は空気や水がきれいで、人々は美しい自然に囲まれている。だから理想は田舎だ。一方で、文化施設や整備された交通システムも欲しい。そういえば、わがまちは田舎にあってそれらもある。つまり、理想とする都市は船橋である。
はい、完成しました！ 教科書のお蔭です。教科書は偉大です。船橋が理想の都市かどうかはさて置き、英作文はこれで満点！
このように授業を進めています。次回は英語表現の授業でのプレゼン課題をどのように作成、解決したか、ご紹介いたします。